¿Sabías que la derivada no es un operador acotado? Aquí puedes encontrar la demostración. Pruebe que el operador $$\begin{array}{r@{\,}ccl} T \colon & \mathcal{C}^1[a,b] & \longrightarrow &\mathcal{C}[a,b]\\ & x & \longmapsto &\displaystyle x’ \end{array} $$ es lineal y no acotado (considerando […]
Sigue leyendoMes: febrero 2020
Cálculo de normas de funcionales 4
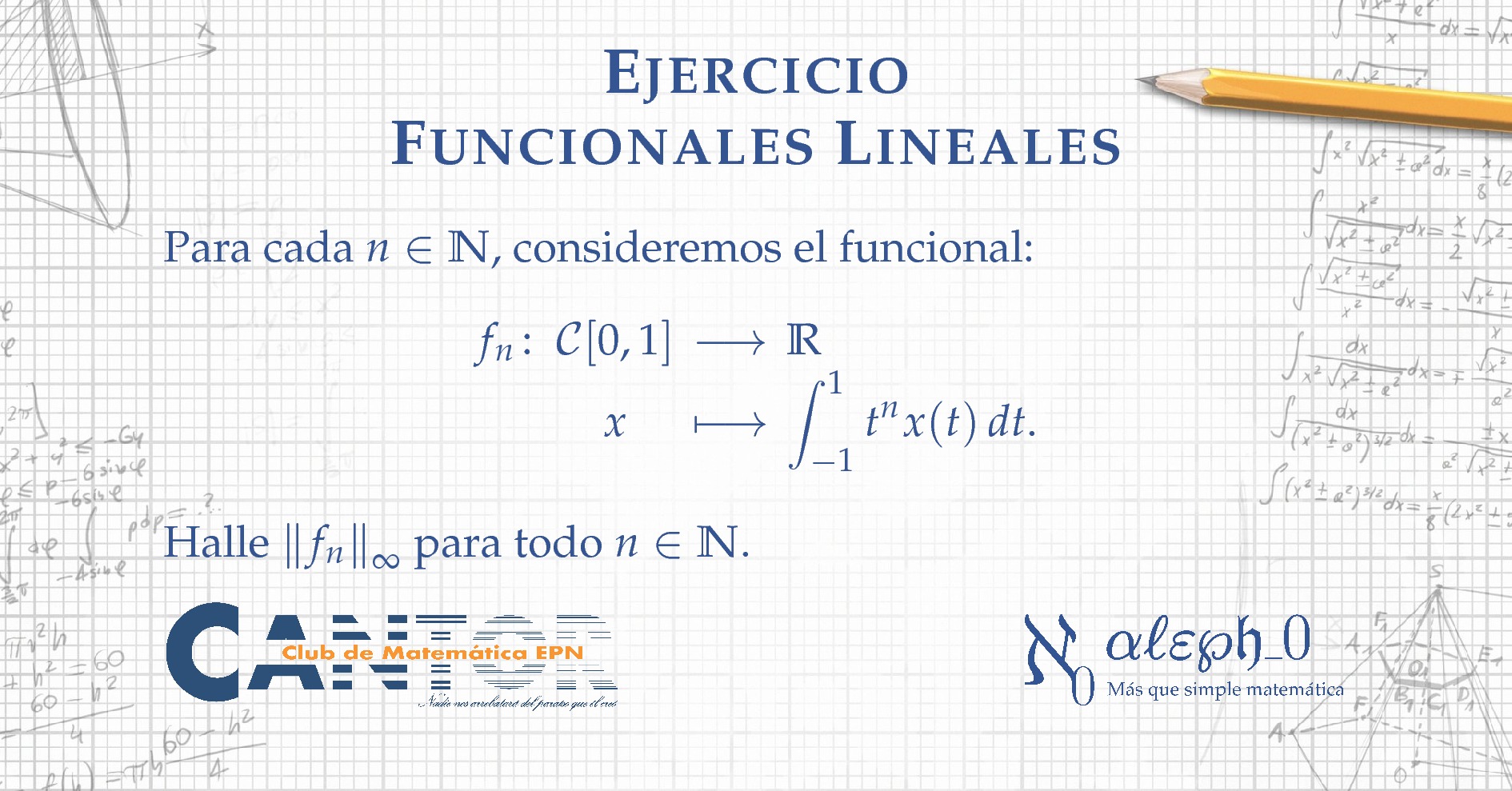
Compartimos este ejercicios de cálculo de normas de operadores lineales que puede serte de utilidad. Para cada \(n\in\mathbb{N}\), consideremos el funcional: $$\begin{array}{r@{\,}ccl} f_n \colon & \mathcal{C}[0,1] & \longrightarrow &\mathbb{R}\\ & x & \longmapsto &\displaystyle \int_{-1}^1 t^n x(t) \, dt. \end{array}$$ […]
Sigue leyendoCálculo de normas de funcionales 3
Compartimos este ejercicios de cálculo de normas de operadores lineales que puede serte de utilidad. Sea \((\mathcal{C}[a,b],\lVert\cdot\rVert_\infty)\), consideremos el funcional: $$\begin{array}{r@{\,}ccl} f \colon & \mathcal{C}[a,b] & \longrightarrow &\mathbb{R}\\ & x & \longmapsto &\displaystyle x(a)-x\left(\tfrac{a+b}{2} \right)+x(b). \end{array}$$ Pruebe que \(f\in \left(\mathcal{C}[a,b]\right)^* […]
Sigue leyendoCálculo de normas de funcionales 2
Compartimos este ejercicios de cálculo de normas de operadores lineales que puede serte de utilidad. Sea \(\rho\in\mathcal{C}[a,b]\) tal que \(\rho(t)>0\), para todo \(t\in [a,b]\). Consideremos el funcional: $$\begin{array}{r@{\,}ccl} f \colon & \mathcal{C}[a,b] & \longrightarrow &\mathbb{R}\\ & x & \longmapsto &\displaystyle […]
Sigue leyendoCálculo de normas de funcionales
Compartimos este ejercicios de cálculo de normas de operadores lineales que puede serte de utilidad. Consideremos el espacio \((\mathbb{K}^n,\lVert\cdot\rVert_2)\), con \(n\geq 2\), y \(a\in\mathbb{K}^n\setminus\{0\}\), para cada \(x=(x_1,\ldots,x_N)\in\mathbb{K}^n\) consideremos el funcional $$\begin{array}{r@{\,}ccl} f_a \colon & \mathbb{K} & \longrightarrow &\mathbb{R}\\ & x […]
Sigue leyendoOperadores acotados y no acotados 2
¿Problemas con demostraciones de operadores acotados y no acotados? Aquí puedes hallar algunos ejercicios que te pueden ayudar. Sean \(E = { x \in \mathcal{C}[a,b]: x’ \in \mathcal{C}[a,b] }\) con la norma \(\lVert x\rVert = \lVert x \rVert_\infty + \lVert […]
Sigue leyendoOperadores acotados y no acotados
¿Problemas con demostraciones de operadores acotados y no acotados? Aquí puedes hallar algunos ejercicios que te pueden ayudar. Sea $$\begin{array}{r@{\,}ccl} I_{pq} \colon & (\mathcal{C}[a,b],\lVert \cdot \rVert_p) & \longrightarrow &(\mathcal{C}[a,b],\lVert \cdot \rVert_q) \\ & x & \longmapsto & x \end{array}$$ con […]
Sigue leyendo