En esta entrada veremos ¿Qué es un Diagrama Sunburst y para qué sirve? ¿Cómo generar un Diagrama Sunburst en Tableau? Ejemplo práctico de Diagrama Sunburst con datos de Ecuador en Tableau. ¿Qué es un Diagrama Sunburst ? Tutorial de generación […]
Sigue leyendoCategoría: Material Nuevo
Lema de Farkas
Teorema 1 (Lema de Farkas). Sean \(A\in\mathbb{R}^{m\times n}\) y \(b\in\mathbb{R}^m\). Entonces, exactamente uno de los siguientes conjuntos debe ser vacío: \(A:=\left\{x\in\mathbb{R}^n\,:\, Ax=b,\, x\geq 0\right\}\); \(B:= \left\{y\in\mathbb{R}^m\,:\,A^Ty\geq 0,\, b^Ty<0\right\}\). Demostración. Sean \(A\in\mathbb{R}^{m\times n}\) y \(b\in\mathbb{R}^m\), cualesquiera. Primera etapa En una primera […]
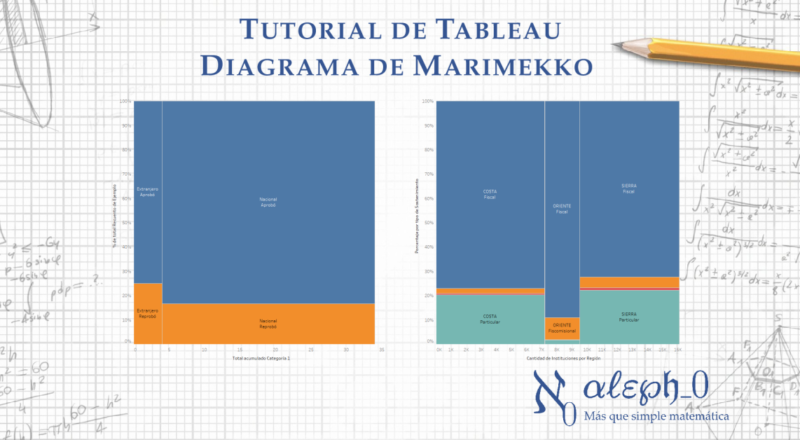
Sigue leyendoDiagrama de Marimekko en Tableau
En esta entrada veremos: Qué es un Diagrama de Marimekko y para qué sirve. Cómo generar un Diagrama de Marimekko en Tableau. Ejemplo práctico de un Diagrama de Marimekko con datos de Ecuador. Videotutorial de Diagrama de Marimekko en Tableau. […]
Sigue leyendoTeorema de Hanh-Banach — Forma Analítica-Algebráica
Teorema 1. Sea \(E\) un espacio vectorial sobre \(\mathbb{K}\), \(F\) un subespacio vectorial de \(E\) y \(g\colon F \rightarrow \mathbb{K}\) un funcional lineal tal que \[\begin{cases} g(x) \leq p(x) & \quad \forall x\in F \quad \text{ si }\quad \mathbb{K}=\mathbb{R}\\ \text{Re}(g(x)) […]
Sigue leyendoApuntes de Python
Compartimos los apuntes de clase del curso «Programación con Python» elaborados por el profesor Luisantos Bonilla Mejía de la Escuela de Matemática de la Universidad de El Salvador.
Sigue leyendo¿Intercambiar la integral y el límite?
Teorema 1. Sean \(\newcommand{\eval}[2]{\Big | _{#1}^{#2}} \newcommand{\Eval}[2]{\Bigg | _{#1}^{#2}}a<b\) y \((f_n)_{n\in\mathbb{N}}\) una sucesión acotada de funciones reales. Entonces \[\lim_{n\to +\infty} \int_a^b f_n(x)\, dx = \int_a^b \lim_{n\to +\infty} f_n(x)\, dx.\] Ejercicio 1. Verifique que \[\lim_{n\to +\infty}\int_0^1 n^2 x^n(1-x)\, dx \neq \int_0^1 […]
Sigue leyendoResumen de Mecánica Clásica I
Junto a Aider EPN, presentamos los apuntes de la clase de Mecánica Clásica I, elaborados por Jhon Chiliquinga y Kevin Cárdenas. Estos apuntes se basan en las clases de la materia «Mecánica Clásica I», dictadas en la carrera de Física […]
Sigue leyendoIntroducción a LaTeX – Guía 01
La filosofía de LaTeX El proceso para la generación profesional de un documento escrito se lo puede dividir en tres etapas: Escritura: es cuando el autor plasma sus ideas concentrándose únicamente es el fondo del documento más no en su […]
Sigue leyendoCálculo de una integral real utilizando una compleja II
Ejercicio. El objetivo de este ejercicio es demostrar que \[ \int_0^{+\infty}\displaystyle\frac{1}{x^4+1}\, dx=\displaystyle\frac{\pi}{2\sqrt 2}. \] Se considera la siguiente gráfica con \(R > 1\), \(z_1=\frac{1+i}{2}\) y \(z_2=\frac{-1+i}{2}\); y tomando \(C = C_1\cup C_2\). Siga los siguientes pasos: Factorice el polinomio \(z^4+1\). […]
Sigue leyendoCálculo de una integral real utilizando una compleja
Ejercicio. El objetivo de este ejercicio es demostrar que \[ \int_0^{+\infty}\displaystyle\frac{1}{x^2+1}\, dx=\pi. \] Se considera la siguiente gráfica: con \(R > 1\) y tomando \(C = C_1\cup C_2\). Siga los siguientes pasos: Calcule \[ \int_C \displaystyle\frac{1}{1+z^2}\, dz. \] Evalúe el […]
Sigue leyendo