Ejercicio 1. Sea \(\alpha\in\mathbb{C}\) tal que \(\mathop{\mathrm{Re}}(\alpha)>1\). Para demostrar que \[\int_0^{+\infty}\dfrac{e^{-t}-e^{-\alpha t}}{t}\, dt =\mathop{\mathrm{Log}}(\alpha).\] vamos a calcular \[\int_C \dfrac{e^{-z}}{z}\, dz,\] donde \(C\) es la curva dada por la unión de \(C_1\), \(C_2\), \(C_3\) y \(C_4\) dadas por la siguiente gráfica […]
Sigue leyendoCategoría: Material Nuevo
Demostración de que un operador cerrado sobre un compacto es acotado
Ejercicio 1. Sean \(E\) y \(F\) espacios normados y \(T\colon E \rightarrow F\) un operador lineal cerrado. Si \(F\) es compacto, demuestre que \(T\) es acotado. Demostración. Primero, notemos que demostrar que \(T\) es acotado es equivalente a demostrar que […]
Sigue leyendoCompletación de una base de Hamel
Ejercicio 1. Sea \(E\) un espacio vectorial sobre \(\mathbb{K}\), \(W\) un subespacio vectorial no nulo de \(E\) y \(B_W\) una base de Hamel para \(W\). Muestre que \(B_W\) puede ser completado a una base de Hamel para \(E\). Demostración. Tomemos […]
Sigue leyendoDemostración de que un conjunto es convexo
Ejercicio 1. Demostrar que el conjunto \[A = \left\{(x,y)\in\mathbb{R}^2:x>0\ \land\ y>\frac{1}{x} \right\}\] es convexo. Primero, consideremos la función \[% { \begin{array}{r@{\,}ccl} f\ \colon & \left]0,+\infty\right[ & \longrightarrow & \mathbb{R}\\ & x & \longmapsto & \displaystyle\frac{1}{x}\ ; \end{array} }\] notemos que, […]
Sigue leyendo¿Cuántos términos tiene el desarrollo de la potencia n de k términos?
¿Cuántos términos tiene el desarrollo de la potencia \(n\) de \(k\) términos? Es decir, al desarrollar \[(a_1+a_2+\cdots+a_k)^n,\] ¿cuántos términos aparecen? Para responder esta pregunta es preciso expresar de forma exacta la pregunta. Ejercicio 1. Dados \(n,k\in\mathbb{Z}^+\) y \(a_0,a_1,\ldots,a_m\) variables distintas, […]
Sigue leyendoError de WolframAlpha al calcular un límite
Ejercicio. Demuestre que el siguiente límite no existe \[ \lim_{(x,y)\to (0,0)} \dfrac{8 x^2 y^3 }{x^9+y^3}. \] Utilizando WolframAlpha, nos indica que este límite es 0: Demostración. De manera simple se puede ver que los límites iterados son igual a \(0\), […]
Sigue leyendoDemostración en una linea de la infinitud de los números primos
En el artículo: A One-Line Proof of the Infinitude of Primes se da la siguiente demostración de la infinitud del conjunto de los números primos: Si el conjunto de números primos \(\mathbb{P}\) es finito, entonces $$0<\prod_{p\in\mathbb P} \mathrm{sen}\left(\frac{\pi}{p}\right)=\prod_{p\in\mathbb P} \mathrm{sen} […]
Sigue leyendo¿La derivada es un operador acotado?
¿Sabías que la derivada no es un operador acotado? Aquí puedes encontrar la demostración. Pruebe que el operador $$\begin{array}{r@{\,}ccl} T \colon & \mathcal{C}^1[a,b] & \longrightarrow &\mathcal{C}[a,b]\\ & x & \longmapsto &\displaystyle x’ \end{array} $$ es lineal y no acotado (considerando […]
Sigue leyendoCálculo de normas de funcionales 4
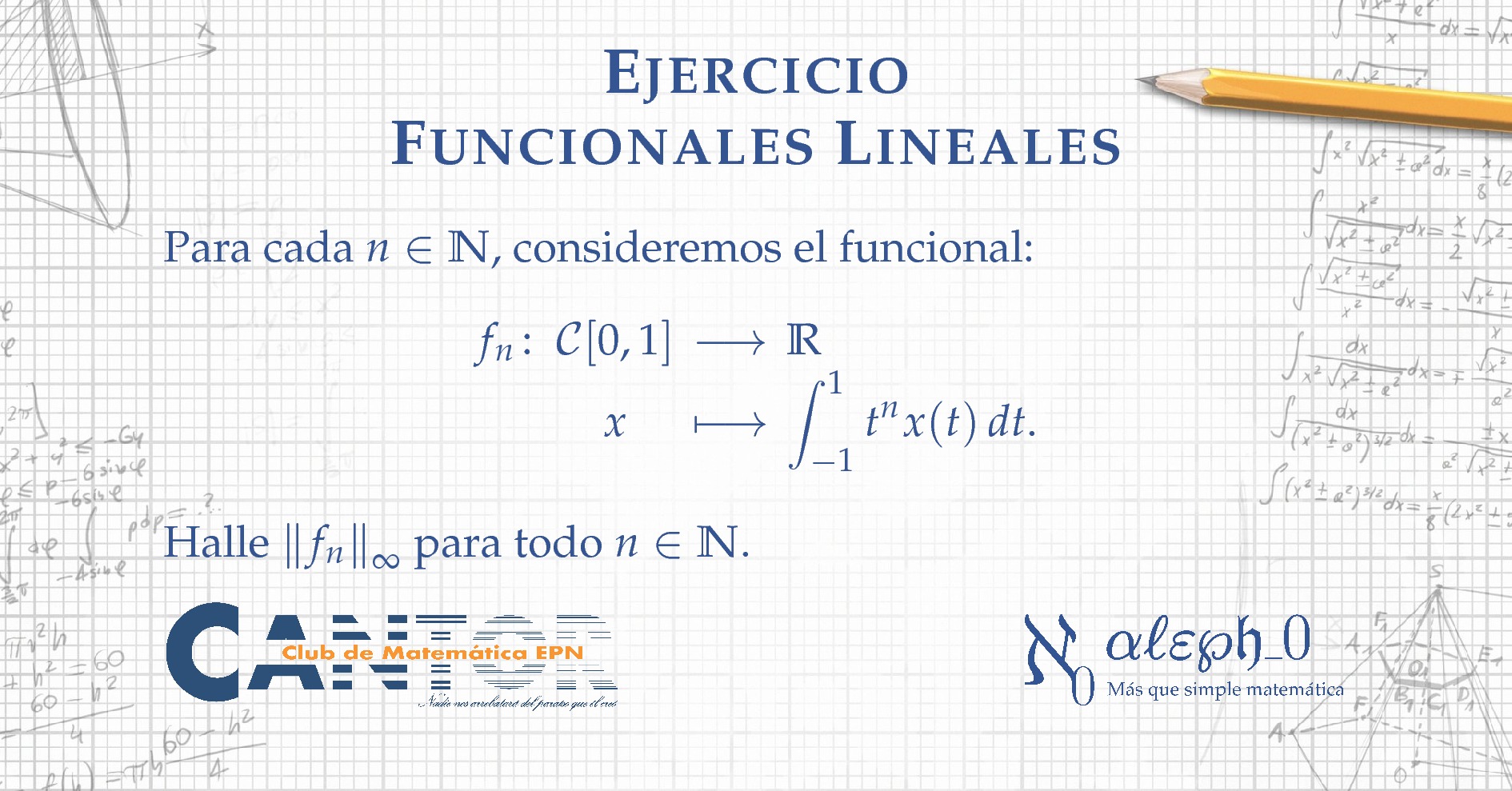
Compartimos este ejercicios de cálculo de normas de operadores lineales que puede serte de utilidad. Para cada \(n\in\mathbb{N}\), consideremos el funcional: $$\begin{array}{r@{\,}ccl} f_n \colon & \mathcal{C}[0,1] & \longrightarrow &\mathbb{R}\\ & x & \longmapsto &\displaystyle \int_{-1}^1 t^n x(t) \, dt. \end{array}$$ […]
Sigue leyendoCálculo de normas de funcionales 3
Compartimos este ejercicios de cálculo de normas de operadores lineales que puede serte de utilidad. Sea \((\mathcal{C}[a,b],\lVert\cdot\rVert_\infty)\), consideremos el funcional: $$\begin{array}{r@{\,}ccl} f \colon & \mathcal{C}[a,b] & \longrightarrow &\mathbb{R}\\ & x & \longmapsto &\displaystyle x(a)-x\left(\tfrac{a+b}{2} \right)+x(b). \end{array}$$ Pruebe que \(f\in \left(\mathcal{C}[a,b]\right)^* […]
Sigue leyendo